英語はかなりマラソンに近い学問です。テスト対策(TOEFL/IELTS対策等の過去問演習)に時間を割けば割くほど英語力の伸びは低下しますが、効率に違いはあれど量に比例して素直に実力は伸びるでしょう。数学ができない人、はたくさんいますが英語は時間さえ丁寧にかけられれば必ず実力は伸びることが保証されています。英語が操れない人、は欧米には居ませんからね。
基本的にreading speedはコツがあるわけではなく量に依存する側面が非常に強いです。
数学はどうでしょうか?
数学は同じ塾へ通ったとしても/参考書を使って取り組んだとしても英語とは異なり顕著に個体差が出ます。同一の参考書を使い学習されたとしても一人は東大に受かり一人はMARCHに不合格する、という現象が数学の場合には起きえます。世間では数学的センスがある、ないと一括りにされますが数学的センスがあるということはどういうことか説明ができますか?
数学学習方法
大学受験時代予備校へ行くという選択肢を私はとりませんでした:数学(その他のほとんどの授業もそうですが)の授業では、ほぼ100%の先生が問題の解説を行います。当時の私は数学は全くできませんでしたが、これらの授業に出て解説を聞いたところで数学ができるようになる事はないだろう、という事は理解できました。
私よりも遥かに数学の才能に溢れている方は世の中に沢山います。今振り返ってみると合格をした多くの人は塾に通っている、という一般常識に囚われずに自分の頭で何が良いかを良く考え、それに基づいて行動することができた為受験では逆転できたんだな、と思います。
授業に出席して受ける解説なら参考書に載っているのでそれを見れば授業に出る意味はありません。高いお金と時間を払って高価な参考書を買っているのと同意義です。
当時の私は参考書を使って学習をしていましたが、当然わからない問題だらけでした。まともに勉強を開始した当時は知らない考え方ばかりでしたので大変勉強になりました。例えば底と高さのそれぞれの2乗を足せば斜辺の2乗になる、という事は知らなければ問題は解けません。この一種定理を自分の頭で考えて捻り出す、ということは一般人には不可能です。
Targetとするテスト(灘中学入学試験や東大入試等)によりexpectationは勿論異なりますが知らなければならない数学的知識というものはやはり存在します。良い知らせはこれらの一種前提となる数学的知識は皆さんが思うほど多くはありません。
一般の方であれば単元毎に最低限抑えておかなければいけないapproach法等は参考書を使ってさっさと抑えてしまった方が効率は良いでしょう。
まずここまでが基礎段階です。
(GMAT/GREで必要とされる基礎知識は順次全てここに公開します。)
しかしだんだん回答を見ても、解き方自体は知っているのに答えが出せない、という状況に陥った為私に数学センスは備わっていないのか…?と悩むと同時に、解答を見て理解するという勉強方法もまたproductiveではないことが理解できました。
数学的センス
ほぼ全てのmath学習者は分からなければ解説を見てor授業に出て理解した上で反復をして対策をします。もし高い数学的センスが備わっていないとすると、解説を見て理解をする、というprocessを繰り返ししてもmath powerは一定のレベルで飽和します。
これが殆どの中学―大学受験生の方が数学で困る理由です。皆さん演習をして復習をすれば良いと思っています。それは残念ながら幻想です。
GMAT/GRE受験生はもう大人です。過去の過ちをなんども繰り返さないでください。
問題集を自習しようが塾や予備校で授業を受けようが世間の殆どの学習者同様に同じ結果に終わるでしょう。
短距離のタイムを縮めたいとします。がむしゃらに腹筋やスクワットでtrainingを積み、校庭を一生懸命に反復して走ればある一定まではタイムは縮まるとは思いますが、生まれ持った素質を上限に途中で伸び悩む結果に終わりますね。
数学において塾や参考書を使って一生懸命反復練習をする、と言うことはそういう事です。
Professional athleteは練習過程において、外部コーチを雇う事で自己のweaknessを意識的に矯正させていくでしょう。仮に数学的才能に溢れていないのであればMath prepでも同じように取り組まなければいけません(全ての学習がそうだと思いますが)。
では数学を学習すると言う事はどう言うことか説明できますか?
パターンを覚える、公式を覚える、できなかったことをできるようにする。
私はどれも違うと思います。
恐らくblog readerの方で中学―大学入試受験者の方は殆どいないと思うのでメインはGMAT/GRE focusにします。
説明に入る前にいくつか問題を解いてみましょう。
GMAT 2020 OG #147
もし小数点第1位から初めて現れる0ではない小数点の数字の間に0が7個以下並んで居るとき、
$$(\frac{t}{1000})^{4}$$
が初めてその条件を満たすときの最小のtの値は?
解けない人のフリをして解いてみます。読み進める前に数学が苦手な方は自分で解いてみましょう。
では解き進めます。
$$t=1, (\frac{1}{1000})^{4}=1\times10^{-12}$$
となります。
0.000…1ですが1が現れるまでに0が何個並ぶでしょうか?
$$1\times10^{-2} =0.01$$
$$1\times10^{-3}=0.001$$
となりますので-12乗の時は小数点には0が11個並びますね。この時点でよくわからないのでもう少し繰り返しをして見ましょう。
$$t=2, (\frac{2}{1000})^{4}=16\times10^{-12}=1.6\times10^{-11}$$
この時0が10個並びます。
$$t=3, (\frac{3}{1000})^{4}=81\times10^{-12}=8.1\times10^{-11}$$
この時も同様に10個ですね。
$$t=4, (\frac{4}{1000})^{4}=256\times10^{-12}=2.56\times10^{-10}$$
おっとtが4になると0の数が9個へ減少しましたね。
どのような時に0の数が減少していくか分析できますか?
もう一ついきましょう:t=6の時は0が何個並ぶか予想できますか?
$$t=6, (\frac{6}{1000})^{4}=1296\times10^{-12}=1.296\times10^{-9}$$
そう、t=6の時はさらに一つ減り0が8個並ぶことが解ります。
一体この問題で何が本質的に聞かれているかがわかりますか?
まずtの値を4乗します。この時にその値の桁数が5桁以上になれば題意を満たすことがわかりますね。9の4乗は6561で4桁であるため最小のtのあたいは10と求めることができます。
この問題の解説を行いたいわけではありませんので次の問題へ行きましょう。少し問題の難易度をあげてみましょう。
開成中学校入学試験問題
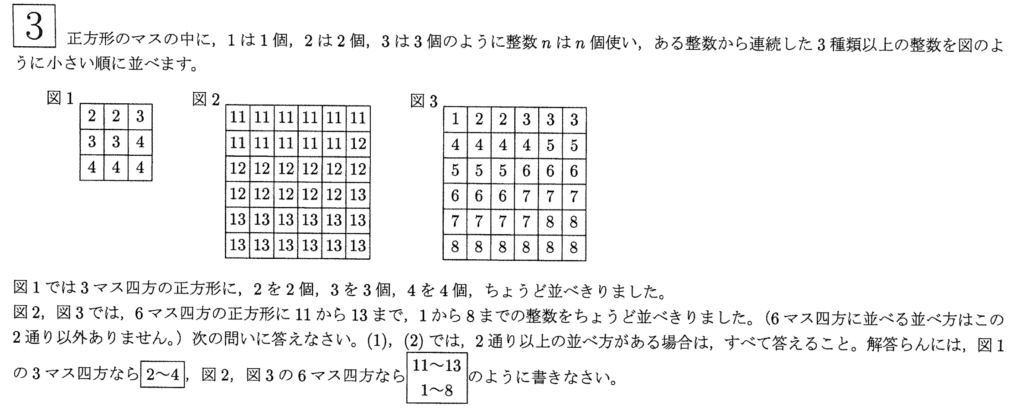
問題: 縦横がそれぞれ10マスの正方形のマスの中に上記のルールにしたがって丁度整数を並べる場合、いくつからいくつまでの整数を並べれば良いかを述べよ。
GMAT/GRE(にしてはちょっと難しいですが)にも出題されるような問題をpickさせて頂きました。解らなくても構いませんのでとにかく頑張って考えてから読み進めてください。かなりの良問です。
では分からない人のフリをして解いてみます。
縦横が10ということは100個の整数が丁度ぴったし100マスに入れば良いわけですね。ちょっとよく分からないので順番に数字を並べてみましょうか。
123を並べると1,2,2,3,3,3となり全部で数字が6個 (この場合マス目が6であれば123を並べればちょうど入るので題意を満たしますね)。
1234を並べると1,2,2,3,3,3,4,4,4,4となりますので全部で数字が10個並びますね。(同様にマス目が10であれば丁度並べられます)
ということは1から5までを並べると15個並ぶ事が見抜けます。これは1から5までを足せば求まりますね。
ではこのまま考察を進めると1から10までをマス目に並べていくと1から10までの数を全て足し合わせれば良いので(1+10)10/2となり整数の数は全部で55となります。マス目が全部で55の場合は1から10までの整数を全て並べればピッタリ入る計算になります。
ここまで見抜けたところで一般化させましょう。では1からnまでの数字を並べた時の数字の合計は幾つでしょうか?1からnまでの数字を並べるとここまでの考察に基づいて(1+n)n/2個数字が並ぶことになります。
1から順に数字を並べて10:10のマス目を埋めにいくと(1+n)n/2=100を満たせば題意を満たす事がわかります。n=14の時は105, n=13の時は91となりますのでどちらも丁度100にはなりません。余るか不足してしまいます。1から順番にn個の数字を並べていくと丁度ピッタリ並べ切る事が不可能である事がわかります。
ということは1から並べ始めるのではなくある途中の数字から並べ始めれば良いのでは?という考察が立ちます。
さらに分析を入れましょう。
123を並べると1,2,2,3,3,3で6個です。
では1をskipして23と並べると2,2,3,3,3で5個数字が並びます。
12345を並べましょう。
1,2,2,3,3,3,4,4,4,4,5,5,5,5,5となり15個数字が並びます。
では1,2をスキップさせて3から並べ始めて345と並べると
3,3,3,4,4,4,4,5,5,5,5,5となりますので12個数字が並びますね。この程度であれば数えればokですが一般化させる必要がありますのでどのようにすれば5個や12個の数字が並んでいると計算で求まるのでしょうか?
23と並べる場合123と並べた時から1の数を引けば5となります。
345のみを並べた場合は同様に12345を並べた場合から12を並べた数を引けば求まりますね(15-3で12個)。
ではこれを一般化させます。Kからnまでの数字を並べた時の合計は幾つになるでしょうか?同様に考えると1からnまでを並べて1からk-1までを並べた数を引けば良い。ということになりますね。
1からnを並べると(1+n)n/2個
1からk-1を並べると上記の式のnをk-1へ取り替えれば良いのでk(k-1)/2個
ではkからnまでの数字を並べた場合(1+n)n/2-k(k-1)/2個の数字がマス目に並ぶことになります。100個のマス目にピッタリ並べ切らなければいけないため
(1+n)n/2-k(k-1)/2=100
を満たすk及びnを求めれば良い事がわかります。2を両辺にかけると
$$n(n+1)-k(k-1)=200$$
$$n^{2}+n-k^{2}+k=200$$
これを因数分解すると
$$n^{2}- k^{2}+n+k=(n-k)(n+k)+(n+k)=(n+k)(n-k+1)=200$$
となります。Kとnが
$$(n+k)(n-k+1)=200$$
を満たすときに題意を満たす事がここまでこれば見抜けます。
AB=200ですので候補としては(1,200),(2,100),(4,50),(5,40),(8,25)の5通りを調べれば良いことになります。
N+k=25, n-k+1=8の時 n=16,k=9
つまり9から16までの数字を並べるとぴったり100マスに収まるわけですね。
他の候補も同様に調べると
N+k=40, n-k+1=5の時n=22 k=18となり題意を満たします。
この2組が正解となります。
これは良い問題ですね!?
Analysis
2つほど問題を解いてみました。
では勉強方法の説明の続きをしましょう。解けない人のふりをして問題を解いてみましたが、まず何故予備校や塾に通う/参考書を使って自習をして実力が打ち止めになるかの説明です。
予備校や塾へ通うこと/参考書を使って答えを見ながら学習をする場合上記2題であれば黒字のみが記載され赤字の箇所はカットされます。
赤字の部分は数学ができる人、数学的センスがあると言われる人のinside of 脳みそor 手元をできるだけ丁寧に残したものになります。赤字の該当箇所で一体数学ができる人たちは何を行なっているか分かりますか?彼らは問題の分析を行なっているわけですね。
例えば1問目でtの4乗の値が5桁になれば良いな、と問題文を読んだ段階でわかっている人は相当少数です。2問目において
$$(n+k)(n-k+1)=200$$
を満たすn and kを求めれば良い、ということを問題文を読んだその瞬間に見抜く事ができるのは超人でしょう。
数学ができる人たちとできない人達では学習している事が全く異なります。
数学ができない人たちは予備校/参考書を使ってできなかった問題の一種解き方を何度も反復させて身に付けようとします。しかし入試を受ければ不合格になりGMAT/GREでは本番点数が取れません。理由は簡単で本番の問題では見た事がない問題に沢山遭遇するとフリーズして手が止まってしまい、解く事ができないからですね。
数学ができる人たちは問題の解き方自体ではなく、日々の学習で赤字部分に該当する問題の分析を演習を通じて反復練習します。私も意識的に鍛えたのはこの部分です。
数学で点数を取って来る人達の場合一見してよく分からない問題に対して分析をかけて来る事でその本質を見抜く事ができます。側から見ていると数学的センスがあるように見えるのですが、これは数学的なセンスがあるかないか、ではなく単純に訓練を積んでいるためできるだけです。頭が必ずしも良いわけではないと思います。
上の問題2つの赤い該当部分を見比べてください。どちらも問題に分析をかけてきていますがそのapproach方法はどちらも酷似しています。どちらの場合もとりあえずよくわからないから1とか2を放り込んで、問題を簡単な設定にして実験をしていますね。
GMAT 50-51/ GRE 157-を安定的に取れる人達でも本番は見たこともない問題に多く遭遇します。どれだけ問題数をこなしても初めて見かける問題を潰せない限り点数向上は望めませんよ。
数学を学習する上で意識的にtrainingしなければいけない事は単純な知識や解き方を身につけていく事ではなく、問題の分析のかけ方です。これは解答を見た上で繰り返し練習をしたり授業を受けても身につく事はないでしょう。英語のreadingの授業解説を受ければそのreadingは読めるのですが、自分でtrainingしない限り別の問題になった途端、英語を読む事はできませんね。解けなくてフリーズしてからどのように問題に分析をかけるのか、数学が苦手な人達はこの引き出しがありません。数学的分析の掛け方は非常に限られていますのでこれを徹底的に練習して向上させてください。
アドバイスとして私は数学ができなかった頃フリーズしてからどのように手を動かして行くか、自分にどのような考え方/分析の仕方ができないのかをノートにまとめました。重要な事は同じような考え方/分析手法を使う問題で何度も間違いを犯さない事です。分からない問題が出てくるたびにノートにまとめた詰め方がapplyできないか?と、当時数学が苦手だった私は意識的に自分のweaknessの矯正を行なっていました。人によって得て不得手必ず一種癖があります。計算ミスをどこでしやすいか、という点も傾向があると思います。自分の数学的なweaknessをどこか説明せよ、と言われて具体的な説明およびその対応方法が説明できる人は数学に苦手意識がある人達の中では居ないと思います。
今まで数学ができない、と思っていたのは数学的なセンスがあるか/ないかの問題ではなく根本的なapproachをただ誤っていただけに過ぎません。
